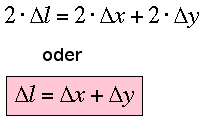
Messwerte physikalischer Grössen sind immer fehlerbehaftet. Wenn nun mit diesen fehlerbehafteten Messwerten Berechnungen durchgeführt werden, dann wird auch das Resultat der Rechnungen eine Unsicherheit aufweisen. Diese Unsicherheit wurde natürlich von den ungenauen Ausgangsdaten geerbt. Man nennt diesen Vorgang Fehlerfortpflanzung. Zunächst soll an zwei einfachen Rechenoperationen, der Addition und der Multiplikation, die Fehlerfortpflanzung erläutert werden.
Wir nehmen an, die Länge l soll gemessen werden, der Massstab dafür ist aber nicht lang genug, sodass die Längenmessung in zwei separate Längenmessungen aufgeteilt wird. Die beiden Teillängen x und y werden danach zur Gesamtlänge l addiert: l=x+y.
Wenn aber nun die beiden Teillängen Fehler x und y aufweisen (systematische, zufällige etc.) dann pflanzt sich dieser Fehler in einen Fehler l der Gesamtlänge l weiter. Die folgende Animation zeigt, wie die Längen x und y variieren und dadurch auch deren Summe l variiert. Um zu ermitteln, wie gross der Fehler der Summe ist, sind die beiden Teilmessungen hintereinander gestellt worden, sodass die Gesamtlänge direkt sichtbar wird.
Nun kann die Variation der Gesamtlänge direkt abgelesen werden, man findet für die Addition fehlerbehafteter Grössen die einfache Fehlerfortpflanzungsregel:
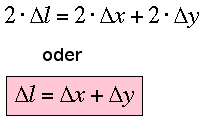
Man spricht in diesem Zusammenhang auch vom maximalen Fehler. Interessanterweise entsteht auch bei einer Subtraktion x-y derselbe maximale Fehler, sodass nun zusammengefasst werden kann:

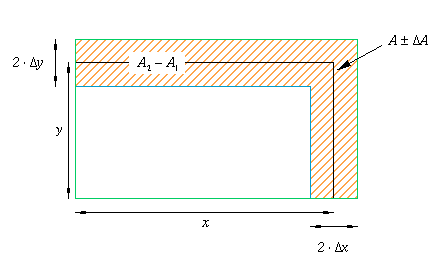
Als Beispiel soll das Produkt aus zwei fehlerbehafteten Grössen x und y ermittelt werden. Dieses Produkt kann als graphisch als Rechtecksfläche A=x·y betrachtet werden. Der folgende Film zeigt die Abhängigkeit der Fläche A von der Variation der Ausgangsgrössen:
Die minimale und maximale Fläche A1 und A2 wird mit den minimalen und maximalen Ausgangsgrössen x und y erzielt. Wenn die Fläche in der Form A± A dargestellt werden soll, dann liefert die Differenz (A2-A1) den Fehler A der Fläche:
 |
 |
Interessanterweise entsteht auch bei einer Division x/y derselbe relative Fehler des Quotenten, sodass nun zusammengefasst werden kann:
