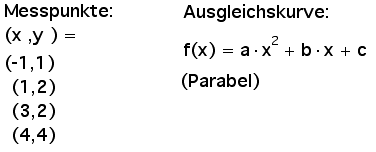
Es soll eine theoretische Kurve optimal an vorgegebene Messpunkte angeglichen werden. Dazu muss die Kurve (Ausgleichskurve, Regressionskurve) von Parametern abhängig sein, deren Werte bei der Anpassung optimiert werden.
Als Beispiel sind unten 4 Messpunkte vorgegeben, und die Ausgleichskurve soll eine Parabel sein, die von drei Parametern a, b und c abhängt.
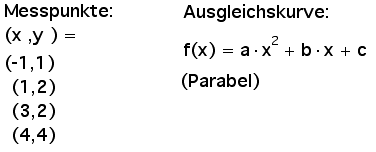
Um die Qualität der Anpassung zu beschreiben verwendet man die Summe der Fehlerquadrate, das heisst die senkrechten Abweichungen der Messpunkte von der Ausgleichskurve werden quadriert und zusammengezählt. Diese Summe ist ein Mass für die Güte der Anpassung. Das Prinzip der kleinsten Fehlerquadrate beruht nun auf dem Wunsch, diese Summe durch Variation der Parameter der Ausgleichskurve möglichst klein zu machen.
Mit der folgenden Animation wird gezeigt, wie die Ausgleichskurve bei unterschiedlichen Parametern mehr oder weniger gut durch die Messpunkte gelegt wird. Als Qualitätsmerkmal der Anpassung dient die Summe der Fehlerquadrate, die bildlich und als Zahl dargestellt ist.
Die Variation der Parameter kann durch direkte Eingabe am Computer geschehen und die Beobachtung der Abweichungsquadrate erlaubt ein optimieren "von Hand". Das folgende Excelbeispiel zeigt zunächst das Aufstellen einer geeigneten Tabelle. Wie üblich sind die entscheidenden Zellenformeln farbig hervorgehoben.

Die folgende Animation zeigt, wie die Variation der Parameter a b und c die Kurvenanpassung ("Kurvenfit") verbessert:
Welche Parameter nun wirklich optimal sind, ist von Hand sehr mühselig zu entscheiden, insbesondere dann, wenn die Parameter nicht ganz unabhängig voneinander optimiert werden können. Deshalb gibt es fertige Optimierungsroutinen, wie zum Beispiel der "Solver" Zusatz bei Excel, die die Optimierung übernehmen. Man muss dazu lediglich die Zielzelle angeben, deren Wert minimiert werden soll, sowie die Zellen mit den Parametern der Ausgleichskurve.
Falls die Messdaten noch unterschiedliche Messgenauigkeiten oder Fehler enthalten, dann können die einzelnen Fehlerquadrate vor der Summenbildung problemlos mit einer Gewichtung versehen werden. Natürlich können auch andere Kurven für die Ausgleichung verendet werden, etwa trigonometrische oder Exponentialfunktionen. Man muss lediglich beachten, dass die Anzahl Ausgleichsparameter kleiner sein muss als die Anzahl Messpunkte. Falls die Ausgleichskurve eine lineare Funktion ist (Gerade), spricht man auch von linearer Regression.