Messwerte physikalischer Grössen sind immer fehlerbehaftet. Die Ursache dafür kann ein charakteristischer Fehler des Messverfahrens oder des Experimentators sein, zum Beispiel eine falsche Eichung des Messgeräts. Meist sind diese Fehler durch sorgfältiges Arbeiten und entsprechende Kenntnisse vermeidbar.
Möglich sind aber auch zufällige oder statistische Fehler, die durch unkontrollierbare Umgebungseinflüsse oder einen zugrundeliegenden zufälligen Prozess erzeugt werden. Oft gehorchen diese zufälligen Fehler statistischen Gesetzmässigkeiten, zum Beispiel der Gauss'schen Fehlertheorie.
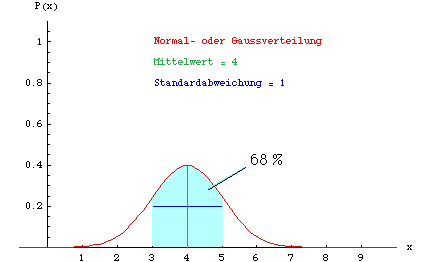
Im folgenden Beispiel soll eine Grösse x (zum Beispiel eine Länge) gemessen werden, deren wahrer Wert x = 4 beträgt. Die Messung soll aber einen zufälligen Fehler enthalten, sodass bei Wiederholung der Messung die Messwerte um den wahren Wert x=4 herum streuen. Man kann diesen Effekt durch eine Verteilungskurve darstellen, die anzeigt, mit welcher Wahrscheinlichkeit benachbarte Werte von 4 herauskommen, wenn man die Messung durchführt.

Die Abbildung zeigt, dass der Wert 4 zwar mit der grössten Einzelwahrscheinlichkeit gemessen wird, dass bei wiederholten Messungen aber die Messwerte mit einer Wahrscheinlichkeit von 68% innerhalb der blau markierten Zone liegen. Für dieses Beispiel wurde eine Standardabweichung von 1 gewählt, entsprechend liegen 68% der Messwerte zwischen 3 und 5.
Normalerweise kennt man den wahren Wert 4 nicht, sondern man versucht ihn durch die Messung zu ermitteln. Weil aber die Einzelmessungen bereits Fehler enthalten, kann nun aufgrund des Messresultats nicht entschieden werden, ob zum Beispiel ein Messwert von 3.527 "zufällig" den wahren Wert darstellt, oder ein zufälliger Fehler mitgemessen wurde. Durch mehrfaches Messen derselben Grösse kann aber die statistische Ungenauigkeit berücksichtigt werden. Das hängt damit zusammen, dass bei jeder Messung der wahre Wert mitgemessen wird und der zufällige Fehler mit positiven und negativen Anteilen zum wahren Wert beiträgt. Je öfter man dieselbe Grösse misst, desto besser kann man abschätzen, wie gross die statistische Streuung ist und wie der zugrundeliegende wahre Wert lautet.
Die Gauss'sche Fehlertheorie sagt dazu, dass die Mittelwertbildung für mehrere Messungen die beste Schätzung für den zugrundeliegenden wahren Wert liefert, und dass die Standardabweichung der Messserie die beste Schätzung für den Fehler einer Einzelmessung darstellt.
Dazu ein Beispiel, welches auch die Rezepte für Mittelwert und Standardabweichung einer Messserie zeigt:

Die Berechnung von Mittelwert und Standardabweichung geschieht am einfachsten mit einem Tabellenkalkulationsprogramm:

Interessant ist bei diesem Beispiel, dass weder der wahre Wert (x=4) noch die wahre Standardabweichung (=1) der Einzelmessung herauskommt, es ist aber die bestmögliche Schätzung aus dem begrenzten Datensatz.
Für die Abschätzung des Fehlers des Mittelwert gibt es ein zusätzliches Rezept:

Es ist klar, dass weitere Wiederholungen der Messung die Genauigkeit der Schätzung für den wahren Wert verbessern. Im folgenden Film wurden die drei bisherigen Messungen erweitert zu einer Serie von 100 Messungen. Für jede Zusatzmessung wurde der Mittelwert und die Standardabweichung des bisherigen Datensatzes ermittelt. Mittelwert (grün) und Fehler des Mittelwerts (blau) sind zusammen mit einer Häufigkeitsverteilung (Histogramm) der Messungen dargestellt. Man erkennt sehr schön die Verbesserung der Qualität des Messresultats.
Das folgende Bild zeigt, wie sich mit steigender Anzahl Messungen der Mittelwert an den wahren Wert annähert. Das spricht natürlich für eine möglichst häufige Wiederholung der Messung.
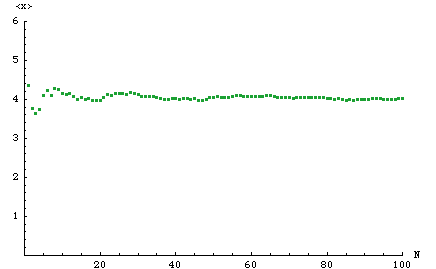
Es muss allerdings betont werden, dass diese Art der Datenauswertung nur bei identischen Messbedingungen durchgeführt werden darf.