
In der Physik werden viele Grössen mit Vektoren dargestellt. Dies betrifft zum Beispiel die Kraft, die Geschwindigkeit, der Drehimpuls, die elektrische Feldstärke, also Grössen, die eine Richtung im Raum besitzen.
Andere physikalische Grössen wie die Masse, die Temperatur oder die Energie besitzen keine Richtung und werden Skalar genannt.
Unten sind zwei Beispiele angegeben, bei denen Vektoren zum Einsatz kommen: links die Bewegung eines Körpers mit dargestellten Geschwindigkeits- und Beschleunigungsvektoren. Rechts ein Vektorfeld, das zum Beispiel ein zeitabhängiges Strömungsbild darstellen könnte:
Doch nun zur Vektorrechnung: die Richtung eines Vektors wird ermittelt, indem er mit den drei Einheitsvektoren im Raum verglichen wird. Die Einheitsvektoren besitzen die Länge 1 (dimensionslos) und verlaufen im kartesischen Koordinatensystem entlang x, y und z.

Ein beliebiger Vektor wird nun in der Komponentenschreibweise als Spalte mit drei Zahlen dargestellt, die angeben um wieviel jeder Einheitsvektor gestreckt werden muss, damit der Vektor gerade die Körperdiagonale im aufgespannten Quader bildet. Die drei Zahlen heissen die Komponenten des Vektors, sie besitzen im allgemeinen eine physikalische Einheit. Wie man sieht, kann auch für die Einheitsvektoren selbst die Komponentendarstellung gewählt werden.
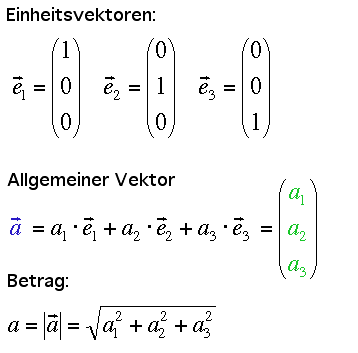
Da der Vektor die Körperdiagonale des roten Quaders darstellt, kann seine Länge bzw. sein Betrag mit Pythagoras berechnet werden.