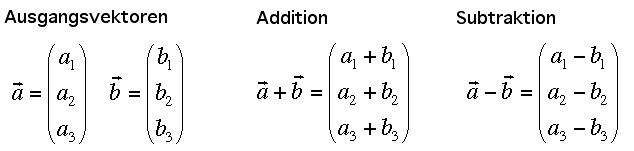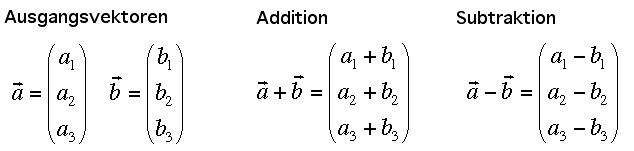Vektoroperationen

In den folgenden Abschnitten werden elementare Operationen der Vektorrechnung demonstriert, jeder Zeitpunkt kann als Übungsaufgabe mit Lösung für die entsprechende Operation benutzt werden.

  • Vektoraddition und Subtraktion:

  • Addition und Subtraktion finden komponentenweise statt:

    • Definitionen:

    Vektordefinition1

    Beispiele:

  • Skalarprodukt

  • Das Skalarprodukt wird oft verwendet, um den Zwischenwinkel zwischen zwei Vektoren zu ermitteln.

    • Skalarprodukt

  • Vektorprodukt

  • Mit dem Vektorprodukt wird ein neuer Vektor berechnet, der senkrecht auf den beiden Faktoren steht und dessen Betrag gleich der Fläche des Parallelogramms ist, das die beiden Vektoren aufspannen. Im ersten Beispiel sind die beiden Vektoren in der x-y Ebene und das Vektorprodukt besitzt nur eine z-Komponente.

    • Skalarprodukt

    Unten ist zur Illustration die allgemeinere räumliche Darstellung gewählt.

    zum Inhaltsverzeichnis