Messwerte sind oft verrauscht, weil zufällige Fluktuationen den Messablauf beeinflussen. In diesem Abschnitt wird exemplarisch demonstriert, wie durch geeignete Signalverarbeitung der Anteil des Rauschens reduziert werden kann.
Es soll eine gedämpfte Schwingung gemessen werden, zum Beispiel das akustische Signal einer angezupften Saite. Je nach Messanordnung kann nun mehr oder weniger Rauschen das Signal überlagern. In der folgenden Animation ist das Signal mit wachsenden Rauschanteilen überlagert worden um das Signal / Rausch Verhältnis (S/N Verhälnis) zu variieren. Gleichzeitig sieht man auf der rechten Seite, wie das Spektrum des Zeitsignals sich ebenfalls verändert.
Man erkennt im rechten Bild, dass sich das Rauschen im gesamten Frequenzbereich verteilt ("weisses Rauschen"). (Klammerbemerkung: Da man sich bei der Digitalisierung des Zeitsignals bereits auf einen Frequenzbereich im Spektrum festlegt, sollte man durch Bandpass-filterung schon vor der Digitalisierung dafür sorgen, dass das Rauschen ausserhalb des Spektrums verschwindet. Ansonsten würde das Rauschen im interessierenden Bereich durch Einfaltung zusätzlich vergrössert.)
Da das Rauschen ebenfalls von der Zeit abhängt, ist im nächsten Bild gezeigt, wie sich bei wiederholten Messungen des Saitenklangs das Messignal und das Spektrum verändern:
Man sieht insbesondere im Spektrum, dass das interessierende Signal bei jeder Messung etwa gleich aussieht: es zeigt nach oben, und besitzt eine klare Frequenz. Das Rauschen aber ist mal positiv, mal negativ und von der Frequenz her unbestimmt.Eine erste Methode zur Verbesserung des Signal/Rausch Verhältnisses ist deshalb die Aufsummierung vieler Messungen. Bei jeder Messung werden die Saitenanteile kohärent addiert, während sich die Rauschanteile teilweise kompensieren. Beachten Sie dazu die folgende Simulation:
Es ist klar, wenn man die Zeit und die Möglichkeit hat, dann sollte man das S/N Verhältnis immer durch Mehrfachmessung zu verbessern versuchen. Speziell beim vorliegenden Beispiel einer gedämpften Schwingung bietet sich aber auch eine weitere Signalverarbeitung an: die Exponentialmultiplikation (evt. in Kombination mit der Aufummierung). Im Zeitsignal der Messungen ist gut erkennbar, dass der Signalanteil zu Beginn der Messung grösser ist als gegen Ende der Messung. Das Rauschen hingegen ist zeitlich konstant. Diese Tatsache kann nun ausgenutzt werden indem man das Zeitfenster unterschiedlich gewichtet: den Anfang stärker als das verrauschte Ende. Dazu multipliziert man das Messignal mit einer abfallenden Exponentialfunktion und danach erzeugt man die Frequenzanalyse und das Spektrum.
Die folgende Animation zeigt diesen Effekt für unterschiedlich starke Exponentialmultiplikationen:
Auch dazu eine Serie von unabhängigen Messungen mit Exponentialmultiplikation:
Man sieht, dass im Spektrum auch die Signalamplitude etwas unter der Exponentialmultiplikation leidet: das Signal wird breiter und niedriger. Allerdings bleibt die Fläche unter dem Signalpeak erhalten. Durch alternative Gewichtungsfunktionen (halbe Gausskurven, Trapezartig..) kann die Peakform im Spektrum etwas beeinflusst werden. Für exponentiell abfallendes Signal wie bei der gedämpften Schwingung ist aber die Exponentialmultiplikation die beste Methode.
Auch hier soll die Aufsummierung des gefilterten Signals demonstriert werden:
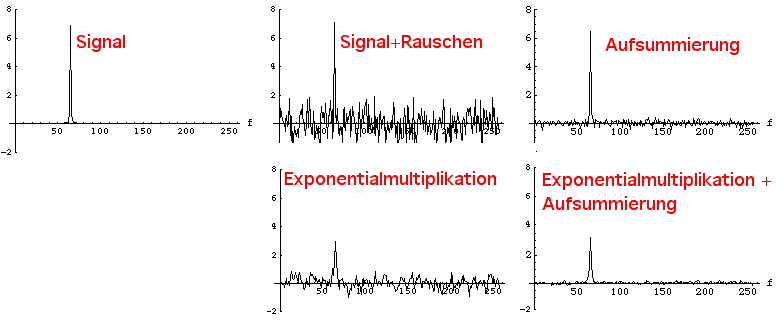
Als Zusammenfassung dieses Abschnitts soll folgende Übersicht dienen:
