Impulserhaltung

Wir betrachten zwei Massenpunkte P und Q, die in gegenseitiger Kraftwirkung stehen. Nach den Newtonschen Gesetzen ist die Kraft auf den Massenpunkt P gleichgross, aber entgegengesetzt gerichtet wie die Kraft auf Q.

Impulserhaltung1

Mit den Beschleunigungen ausgedrückt:

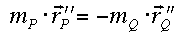
Impulserhaltung2

Alles auf eine Seite genommen:

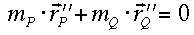
Impulserhaltung3

Die zeitliche Änderung ist Null, somit ist die folgende Grösse zeitlich konstant:

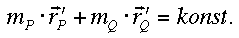
Impulserhaltung4

Sie kann Impulssumme, oder Gesamtimpuls genannt werden.

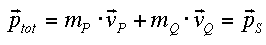
Impulserhaltung5

(Mit der Definition des Schwerpunkts sieht man auch, dass dies auch gerade der Impuls des Schwerpunkts ist.)

Der Gesamtimpuls ist also zeitlich konstant, wenn zwei Massenpunkte Kräfte aufeinander ausüben, und keine weiteren (äusseren) Kräfte wirken.

Dieser Satz kann auch auf grössere Systeme verallgemeinert werden:

Impulssatz: Wenn ein System von Massenpunkten nur inneren Kräften unterliegt, ist die Impulssumme (= Schwerpunktsimpuls) zeitlich konstant.

Die folgenden Simulationen zeigen solche Systeme, die nur inneren Kräften unterworfen sind. Der Schwerpunkt (das kleine Kreuz) wird dabei nicht beschleunigt.

  • Vier unterschiedliche Körper sind über Federn miteinander verbunden. Es sind keine weiteren Kräfte vorhanden. (Dies könnte als mechanisches Modell eines Moleküls dienen). Während die einzelnen Teile des Systems wilde Bewegungen vollführen, bleibt der Schwerpunkt davon völlig unberührt.

  • Auch Explosionen setzen innere Kräfte frei. Der Schwerpunktsimpuls bleibt dabei konstant. Im folgenden Beispiel fliegt eine Rakete weg, und explodiert nach einer halben Sekunde. Die Bruchstücke fliegen aufgrund der inneren Kräfte davon, der Schwerpunkt folgt aber dem Trägheitsgesetz:

  • Im vorhergehenden Beispiel waren keine weiteren Kräfte vorhanden. Falls aber die Schwerkraft (als äussere Kraft) auf die einzelnen Bruchstücke wirkt, dann folgt auch der Schwerpunkt einer Wurfparabel:

  • Gasteilchen stossen an die Wand eines Volumens und üben dadurch Kraftstösse und Druck auf die Wände aus. Auch bei diesen Stössen unterliegt das System Gasbehälter - Gas nur inneren Kräften, sodass sein Schwerpunkt nicht beschleunigt wird. Hier ist ein Beispiel mit nur zwei Teilchen gezeigt:

    • Weitere Beispiel werden bei den Stössen gezeigt.

    zum Inhaltsverzeichnis