
Unter der Dispersion von Wellen versteht man die Abhhängigkeit der Phasengeschwindigkeit von der Wellenlänge. Die Phasengeschwindigkeit ist die Geschwindigkeit mit der sich die Nullstellen einer harmonischen Wellen fortbewegen.
Bei einer harmonischen Welle der Form:

lässt sich der Zeitverlauf animieren:
Oft wird die harmonische Welle mit der Schwing-Kreisfrequenz omega und der Wellenzahl k dargestellt:
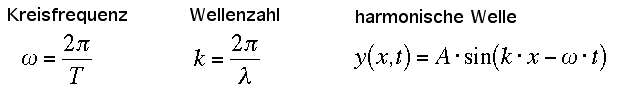
Die Phasengeschwindigkeit wird berechnet, indem man die Wellenlänge (Strecke) durch die Schwingungsdauer (Zeit) dividiert. Alternativ kann man auch omega und k verwenden:
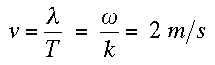
Wenn man die Wellenlänge und die Periodendauer dieser Welle in einem Diagramm darstellen möchte, erhält man zum Beispiel folgende Darstellungsmöglichkeiten.
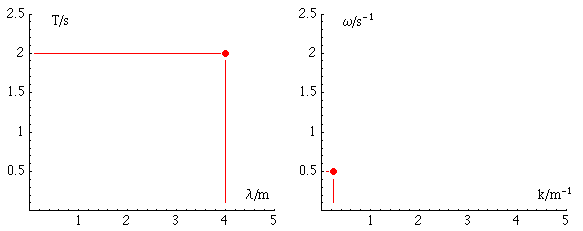
Alle Wellen, die auf einer Geraden durch den Ursprung im omega-k Diagramm liegen, besitzen dieselbe Phasengeschwindigkeit. Die Steigung der Geraden ist gerade diese Geschwindigkeit.
In der folgenden Animation sind 4 Wellen mit unterschiedlichen Wellenlängen, Frequenzen und Ausbreitungsgeschwindigkeiten gezeigt. Daneben sind die Wellen durch Punkte im T - lamda bzw. omega - k Diagramm gezeigt.
Wir betrachten nun eine mechanische Kompressionswelle, zum Beispiel eine Schallwelle durch eine Federkette, und leiten den Zusammenhang w - k her.
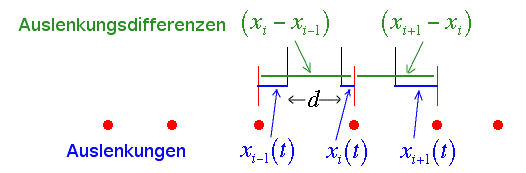
Bei einer harmonschen Welle haben die Auslenkungen aus der Ruhelage folgende Form:
Wir berechnen nun die Federkraft auf das i-te Teilchen. Wir berücksichtigen dazu nur die nächsten Nachbarn und nehmen Hooke'sche Federkraft der Federkonstanten f an. Der Ruheabstand der Teilchen ist d, die Differenz der Auslenkungen bestimmt die Federkraft auf die einzelnen Teilchen.
Ein Standbild aus dem Film:
Wenn wir harmonische Wellen entlang der Federkette berechnen wollen, soll die Auslenkung der Teilchen wie folgt aussehen:
Das Aktionsprinzip von Newton liefert die Bewegungsgleichung, die in diesem Fall durch Ableitung und die Additionstheoreme weiter umgeformt werden kann:
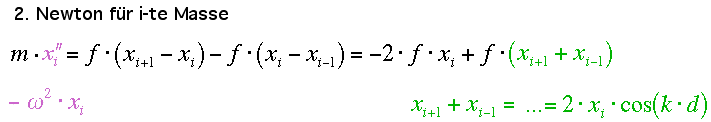
Dies kann nun nach omega aufgelöst werden und liefert die gesuchte Dispersionsrelation:
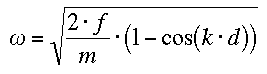
Wie man sieht verläuft die Kurve im Diagramm nicht als Gerade, somit zeigt die Federkette Dispersion. Variation der Federstärke bzw. Masse streckt die Dispersionskurve nach oben, Variation der Gitterkonstanten d staucht die Kurve in horizontaler Richtung.
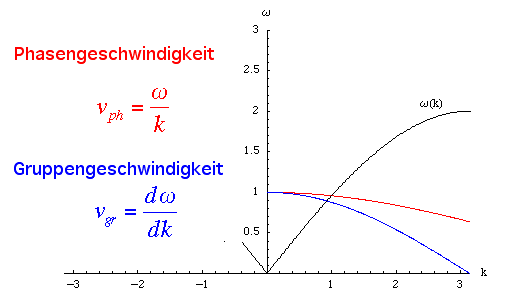
Wellen mit grossem k-Wert (kleiner Wellenlänge) laufen etwas langsamer. Bei sehr grossen Wellenlängen in der Nähe von k = 0 ist die Dispersion klein, die Phasengeschwindigkeit entspricht genau dem Resultat, das aus der Theorie der Schallwellen stammt:

Wenn Wellenpakete aus harmonischen Wellen aufgebaut werden, dann ist die Gruppengeschwindigkeit die Ableitung der Dispersionskurve nach k. In der Nähe von k = 0 (grosse Wellenlänge) ist die Gruppengeschwindigkeit gleich gross wie die Phasengeschwindigkeit, bei sehr kurzwelligen Wellen sinkt die Gruppengeschwindigkeit gegen Null.
Interessant ist schlieslich auch die Frage, welche k-Werte überhaupt eingenommen werden können. Die kürzeste Wellenlänge, die nach dem Sampling-Theorem durch Punkte der Federkette dargestellt werden kann, ist:
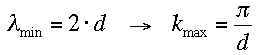
Da die Wellen am Ende des Wellenträgers reflektiert werden, ist die längste harmonsche Welle die stehende Welle der Grundschwingung, sie besitzt die Wellenlänge:

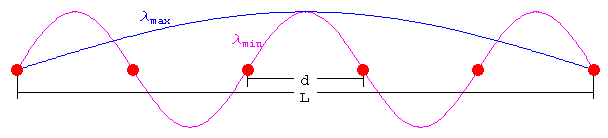
Weitere k-Werte sind aus demselben Grund ganzzahlige Vielfache von kmin.
Bei Variation von den einzelnen Gitterparametern ändert sich die Dispersionskurve und die realisierten k-Werte wie folgt: