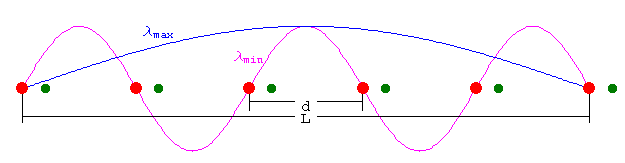
Die Bewegung von Teilchen in einem Kristall kann mit ähnlichen Überlegungen beschrieben werden, wie sie im Kapitel Dispersion (Wellenlehre) demonstriert wurden. Hier soll aber die Situation gezeigt werden, wenn die Elementarzelle mehr als ein Atom enthält. Wir wählen wiederum die lineare Federkette zum Einstieg.
Bezeichnungen:

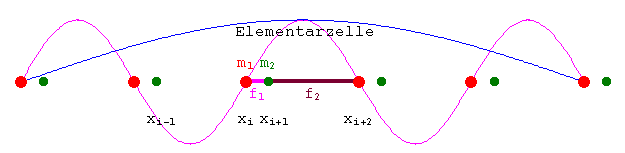
Wenn die Elementarzelle aus zwei Atomen besteht, dann muss die Bewegungsgleichung für die beiden Massen separat aufgeschieben werden.
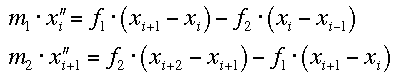
Wir suchen Lösungen, die als harmonische Wellen mit Wellenzahl k (bzw. q = k·d) über die einzelnen Elementarzellen läuft, deshalb besitzen die Teilchen in benachbarten Elementarzellen eine feste Phasenbeziehung:
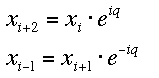
ausserdem soll die stationäre Lösung gesucht werden, bei der alle Teilchen mit der Frequenz omega schwingen.
Das führt zu folgendem Gleichungssystem:
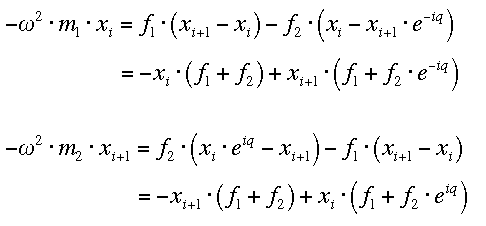
das als Eigenwertproblem gelöst werden kann (E = Einheitsmatrix):
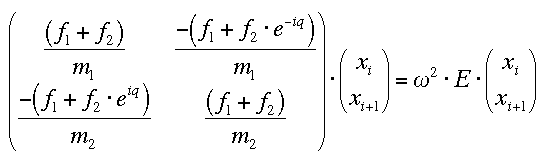
Die Lösungen sind Linearkombinationen von Schwingungen der beiden Teilchen der Elementarzelle, die einen eindeutigen Zusammenhang zwischen k und omega besitzen. Dieser Zusammenhang wird als Dispersionsrelation bezeichnet.
Bei Variation von den einzelnen Gitterparametern ändert sich die Dispersionskurve und die realisierten k-Werte wie folgt:
Im Unterschied zum Resultat im Kapitel Dispersion, kommt es nun auch zu hochfrequenten Schwingungen mit kleinen k-Werten. Dieser sogenannte optische Zweig in der Dispersionskurve rührt von Schwingungen innerhalb der Elementarzelle. Im akustischen Zweig hingegen ist Bewegung innerhalb der Elementarzelle einigermassen gleichphasig.
Sehr instruktiv sind die Schwingungen im Zeitverlauf, die zu den einzelnen Punkten in der Dispersionskurve gehören:
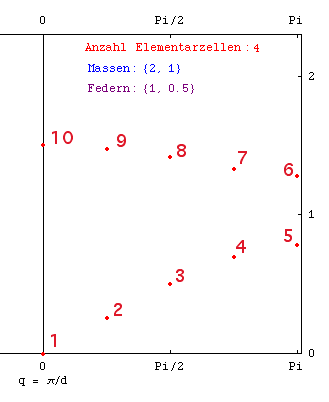 |
Wenn mehr als zwei Gitterpunkte die Elementarzelle bilden, entstehen weitere optische Zweige. Zum Beispiel bei 4 Teilchen pro Elementarzelle erhält man folgendes Bild:
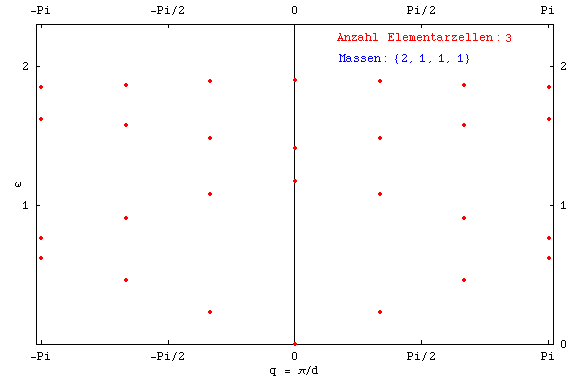
Einzelne Schwingungsformen sehen wie folgt aus: