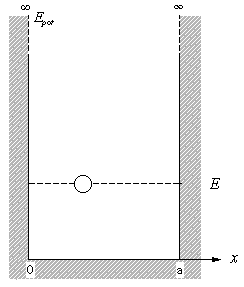
Wenn ein klassisches Teilchen zwischen zwei ideal reflektierenden Wänden eingesperrt wird, so wird das Teilchen sich regelmässig hin und her bewegen, bei jedem elastischen Stoss kehrt sich sein Impuls um, die Energie bleibt konstant. Das ausserhalb der Wände liegende Gebiet besitzt wesentlich höhere potentielle Energie als die kinetische Energie des Teilchens und kann vom klassischen Teilchen nicht erreicht werden. Man spricht auch von einem Kastenpotential.
Ein Elektron in einem Atom, ein Proton im Atomkern oder ein Gasmolekül in einem begrenzten Gasraum sind Beispiele für mikroskopische Teilchen, die in einem endlichen Raumbereich eingesperrt sind. Die zugehörige potentielle Energie soll der Einfachheit halber im erlaubten Bereich Null sein und ausserhalb unendlich gross. Man spricht dann auch von einem Kastenpotential oder Potentialtopf.

Die klassische Vorstellung eines Teilchens mit zugehörigem Ort und Impuls muss jedoch fallengelassen werden; in der Quantenmechanik wird das Teilchen durch eine komplexe Wellenfunktion dargestellt, deren Absolutwert der Aufenthaltswahrscheinlichkeit des Teilchens entspricht. Die Zeitentwicklung der Wellenfunktion wird in der Quantenmechanik durch die zeitabhängige Schrödingergleichung berechnet.
Für die folgende Animation wird ein lokalisiertes Wellenpaket konstruiert, das gegen die rechte Wand im Kasten läuft. Gezeigt ist der Absolutwert der Welle. Man sieht, dass das Wellenpaket im Laufe der Zeit auseinanderfliesst und dass die Reflexion am Potentialwall zu komplizierten Welleninterferenzen führt. Nach einer Weile kann das Teilchen zwischen den Wänden nicht mehr genau lokalisiert werden.
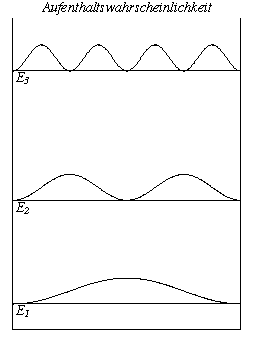
In den elementaren Kursen der Quantenmechanik werden meist die zeitunabhängigen Lösungen der Schrödingergleichung gesucht. Die stationären Zustände entsprechen stehenden Wellen mit festen Werten für die Energie. Diese Eigenfunktionen können wie bei einer schwingenden Saite sichtbar gemacht werden. Sie werden so in die Kastenbreite a eingepasst, dass eine ganze Anzahl Halbwellen Platz findet. Dies ist nur für diskrete Wellenlängen möglich, entsprechend ist auch die Frequenz und die zugehörige Energie quantisiert.
Der Film zeigt die ersten drei Eigenfunktionen in Bewegung. Daneben ist die Aufenthaltswahrscheinlichkeit als Quadrat der Amplituden der Wellenfunktion abgebildet. Die Höhe deutet die Energie des Zustands an.
Interessant ist, dass bei Verringerung der Kastendimension a die Energiezustände ihren Abstand vergrössern. Ebenso wird die Nullpunktsenergie, die zum tiefsten Energiezustand gehört, grösser. Die folgende Animation zeigt dies:
Im Grunde genommen ist das Potentialkasten ein dreidimensionaler Bereich, in dem das Teilchen sich aufhalten muss. Lediglich der Übersicht halber wurde oben die eindimensionale Darstellung gewählt. Unten sind nun die ersten drei Eigenzustände in zwei Dimensionen gezeigt. Man sieht jeweils rechts die Aufenthaltswahrscheinlichkeiten, die bereits an Orbitale in Atomen erinnern.


